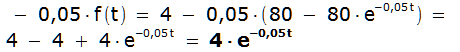Wachstum

Themen:

• Exponentielles Wachstum

• Exponentielle Abnahme

• Beschränktes Wachstum

• Logistisches Wachstum

• Modellieren bei gegebenen Daten

• Übungsaufgaben

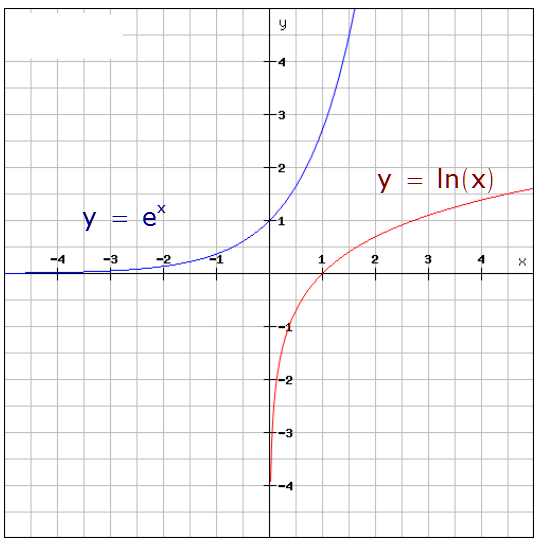
Exponentielles Wachstum

Beispiel: Wachstum des Durchmessers eines Baumes

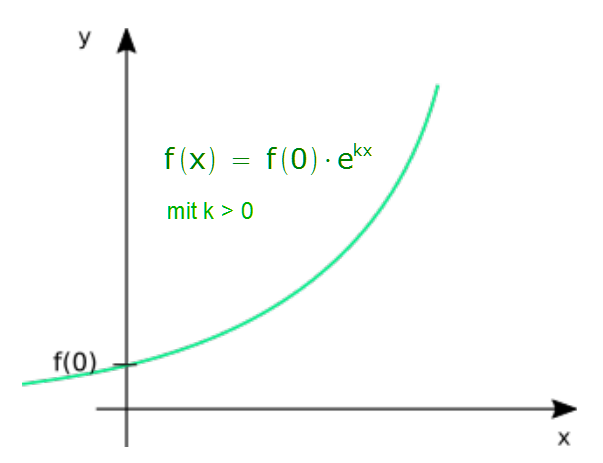
Bestandsfunktion:

mit k > 0

Die Bestandsfunktion f (x) ist Lösung der Differentialgleichung:

f '(x) repräsentiert die Änderungsrate.

Verdopplungszeit bei exp. Wachstum

Wenn die Variable x die Zeit beschreibt, wählt man

als Variablennamen häufig "t" statt "x".

Sei t_D die Zeit, in der sich der Bestand verdoppelt, dann gilt:

→

→ →

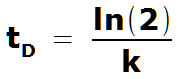
Exponentielle Abnahme

Beispiele exponentieller Abnahme: Radioaktiver Zerfall,

Abnahme Helligkeit im Wasser

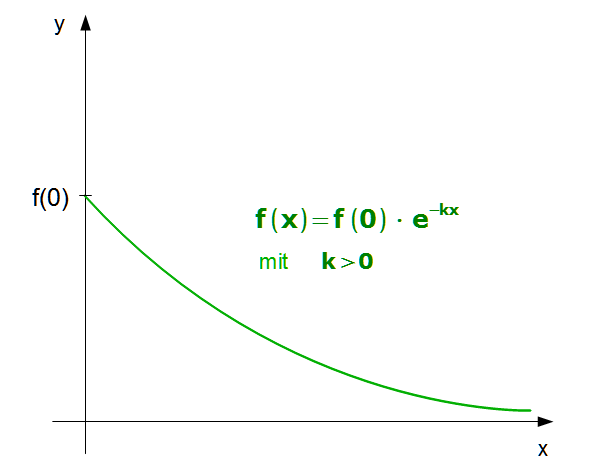
Bestandsfunktion:

mit k > 0

Halbwertszeit bei exponentieller Abnahme:

Sei t_H die Zeit, in der sich der Bestand halbiert, dann gilt:

→

→ →

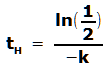
Beachte: Es ist t_H > 0, da < 0 und k > 0 sind.

Beschränktes Wachstum

Man unterscheidet die Fälle

• Bestand kleiner Schranke

  Beispiel: Wachstum Bakterienkultur in einer Petri-Schale.

• Bestandgrößer als Schranke

Beispiel: Abkühlung einer Flüssigkeit auf Zimmertemperatur.

Bestandsfunktion: mit k > 0 und c = f(0) - S

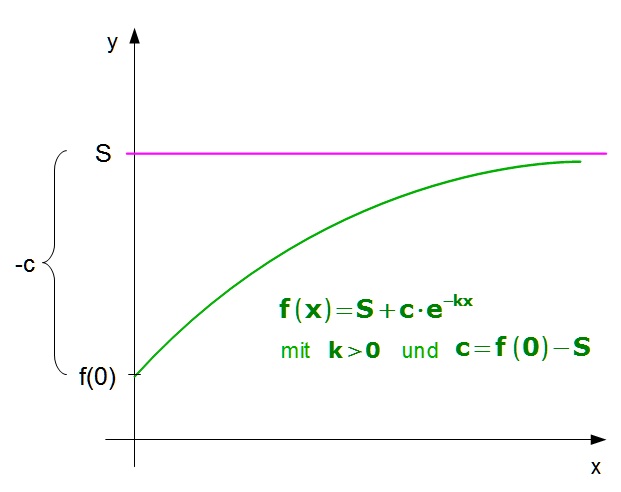
Bestand kleiner als Schranke

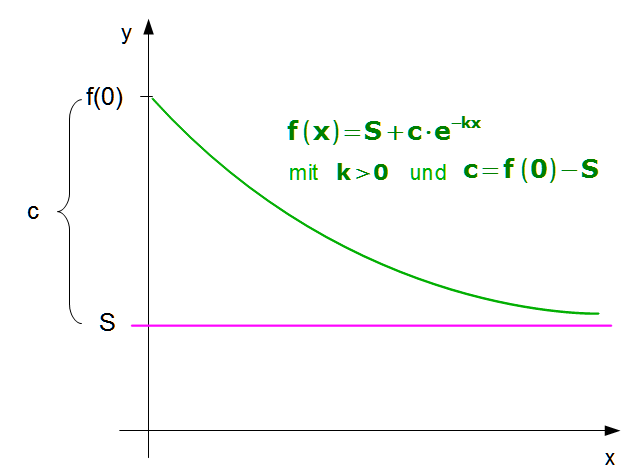
Bestand größer als Schranke

Die Bestandsfunktion f (x) ist Lösung der Differentialgleichung:

Die Funktionheißt Manko-Funktion.

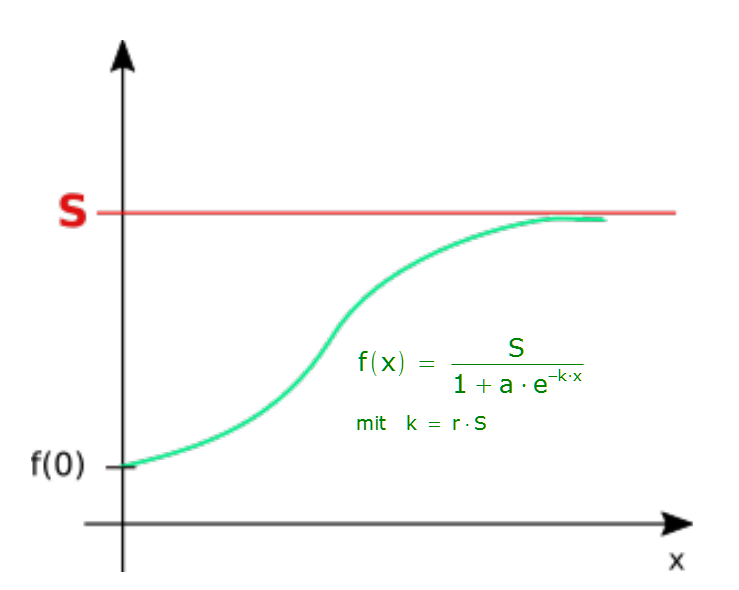
Logistisches Wachstum

Beispiel: Ausbreitung einer Infektion.

Differentialgleichung:

d.h. die Änderungsrate ist proportional zu f(x) und (S - f(x)).

Bestandsfunktion:

Modellierung bei gegebenen Daten

Es geht hier darum, zu einer gegebenen Menge von

Daten, einen Ansatz für eine geeignete Bestandsfunktion

zu bestimmen.

Beispiel 1

Da die Änderungsrate relativ konstant ist,

machen wir den Ansatz:

Es liegt eine Differentialgleichung für exponentielles

Wachstum vor mit der Lösung

Aus erhält man

bzw.

Beispiel 2

Gegeben sie die Datenreihe entsprechend den

Zeilen 1 u. 2 nachfolgender Tabelle.

Wir prüfen, ob ein Ansatz als beschränktes Wachstum

sinnvoll ist.

Als obere Schranke kann S = 1000 angenommen werden.

Das "Manko" M(t) sei definert als M(t) = S - A(t).

Aus der letzten Zeile geht hervor, dass für die

Änderungsrate von M(t) gilt: ,

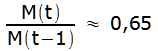d.h. für M(t) kann exponentielle Abnahme angenommen

werden:

( mit k < 0 )

Für die Bestandsfunktion ergibt sich

,

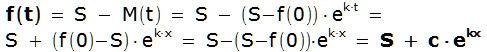also die Formel für beschränktes Wachstum.

Übungsaufgaben

A1 Abnahme der Helligkeit im Wasser

Bei einem See mit klarem Wasser nimmt die Helligkeit

unter der Wasseroberfläche ab; in 1m Tiefe beträgt sie

noch 80% des Wertes an der Oberfläche. Der Verlauf

der Helligkeitsabnahme kann als exponentielle Abnahme

angesehen werden.

a) Bestimme eine Modellfunktion für die Helligkeit unter

Wasser, wenn die Helligkeit an der Oberfläche

400 Lux beträgt.

b) Wie groß ist die Helligkeit in 10m Tiefe?

c) Wo beträgt die Helligkeit nur noch 50% (der

Helligkeit an der Oberfläche)?

d) In welcher Tiefe beträgt die Änderungsrate -7 Lux?

Lösung a)

Ansatz mit f(0) = 400, k > 0 .

→

→

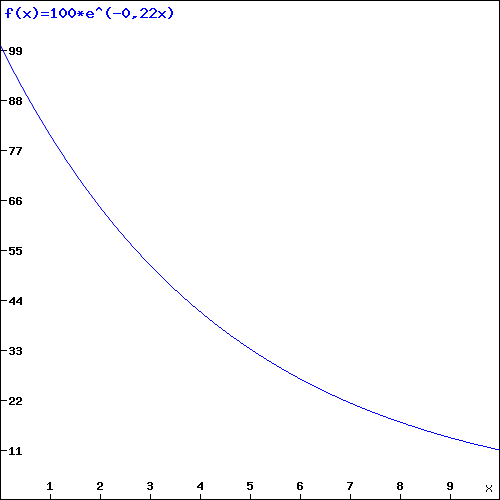
Lösung b)

Lösung c)

Lösung mit Halbwertsformel

Allgemein gilt ,

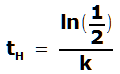also hier:

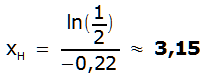
Lösung mit Herleitung

Ansatz

→

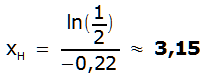
Lösung d)

Die Änderungsrate entspricht der Ableitung von f(x), also

↔

↔

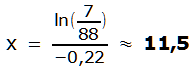
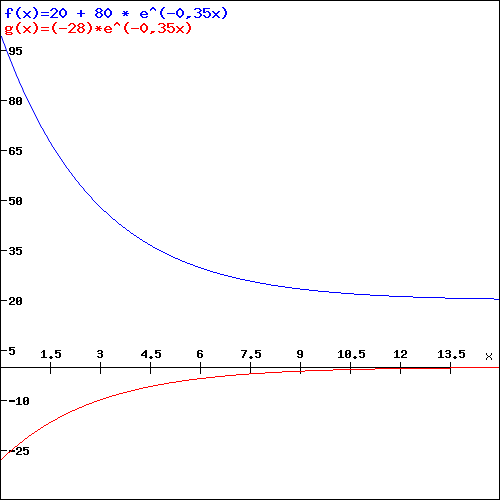
A Erwärmung einer Flüssigkeit

Ein Flasche Sprudel mit der Temperatur 8⁰C wird aus
dem Kühlschrank genommen und im Freien, wo die

Temperatur 30⁰C beträgt, hingestellt. Nach 12 Minuten
beträgt die Temperatur des Sprudels 15⁰C.

Es wird davon ausgegangen, dass die Erwärmung
nach dem Gesetz des beschränkten Wachstums erfolgt.

a) Stelle die Funktion
"f(x) = Temperatur nach x Minuten" auf.

b) Wie hoch ist die Temperatur nach 5 Minuten?

c) Wie lange muss man warten, bis sich die
Temperatur auf 20⁰C erwärmt hat?

d) Wann beträgt die Erwärmung des Sprudels
0,5⁰C pro Minute?

Lösung a)

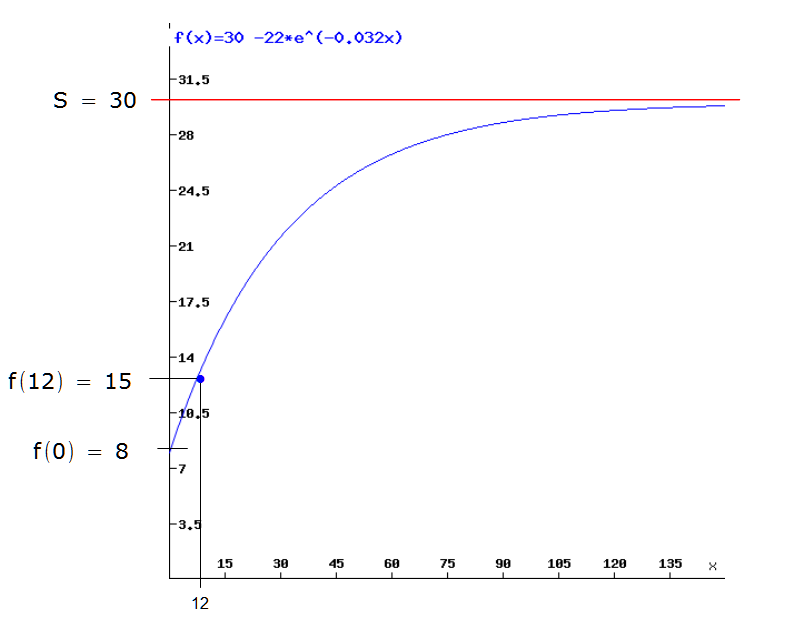
mit und k > 0

f(12) = 15 →

→

→

Die Bestandsfunktion lautet somit

.

Lösung b)

Lösung c)

→

→

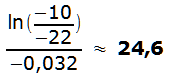
Lösung d)

Die gesuchte Erwärmung entspricht der Änderungs-

rate, d.h. der Ableitung der Bestandfunktion.

→

→

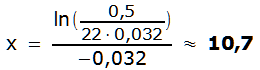
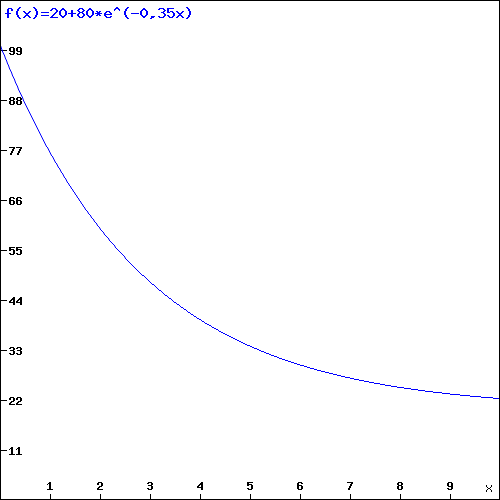
A3 Abkühlung einer Flüssigkeit

Ein Tee wird mit kochendem Wasser aufgegossen

und in einem Raum mit 20⁰C abgestellt.

Nach 2 Minuten ist der Tee auf 60⁰C abgekühlt.

a) Stelle die Funktion
"f(x) = Temperatur nach x Minuten" auf.

b) Wie hoch ist die Temperatur nach 1 Minute?

c) Wie lange muss man warten, bis sich die
Temperatur auf 50⁰C gesenkt hat?

d) Wann beträgt die Abkühlung des Tees
0,5⁰C pro Minute?

Lösung a)

mit und k > 0

f(2) = 60 →

→

→

Die Gleichung für die Bestandsfunktion lautet:

Lösung b)

Lösung c)

Beachte: Die Formel für die (einfache) exponentielle
Abnahme (ohne Schranke) kann hier nicht

angewendet werden!

↔

↔

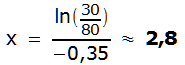
Lösung d)

↔

↔

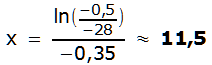
A4 Lösung einer Differentialgleichung bestimmen

Bestimme eine Lösung für die Differentialgleichung

(*) .

Lösung

Durch Ausklammern erhält man .

Dies ist eine Differentialgleichung für beschränktes Wachstum;

Lösung: .

Nachweis:

Es wird gezeigt, dass beide Seiten von (*) gleich sind.